The Conic Sections
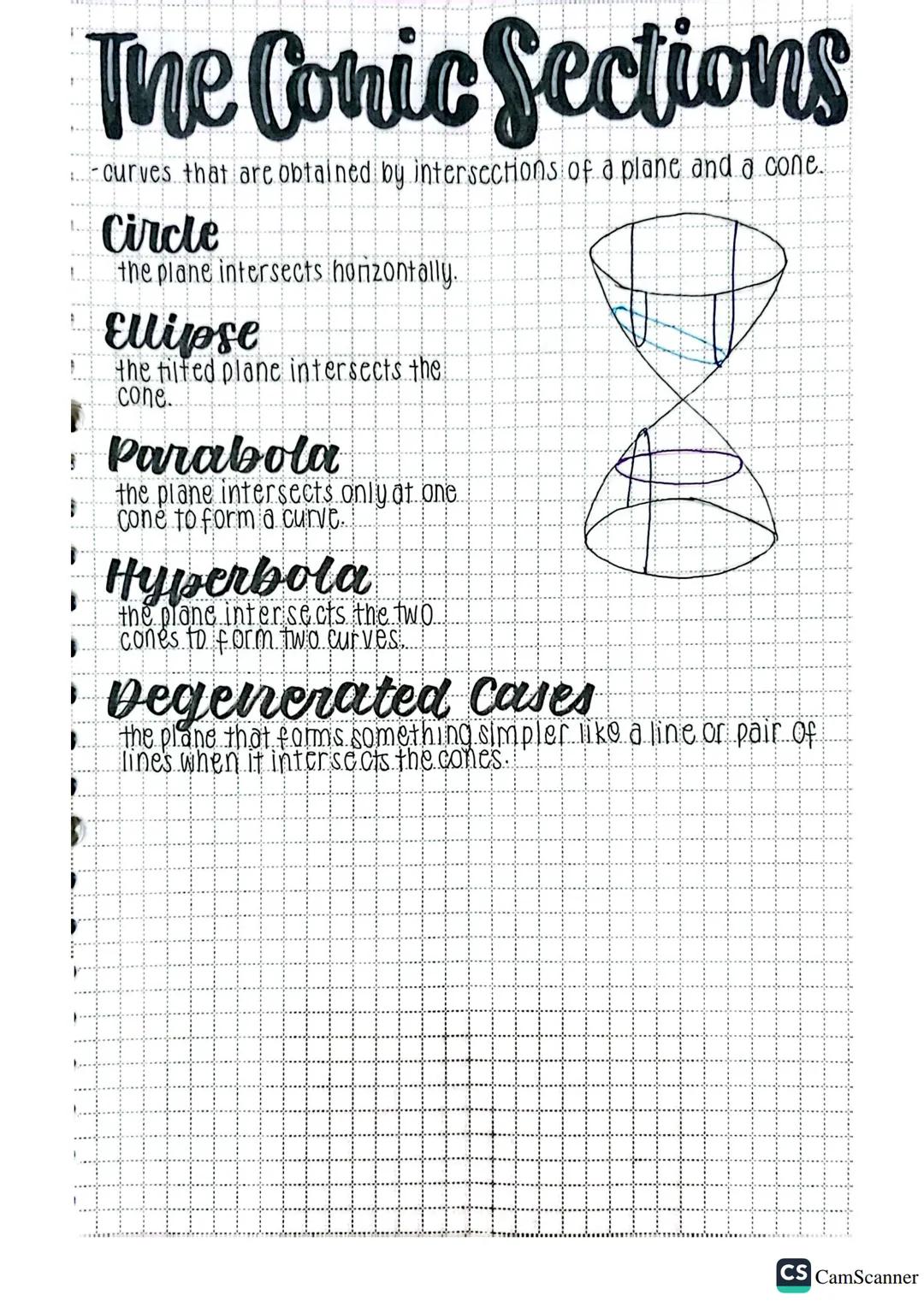
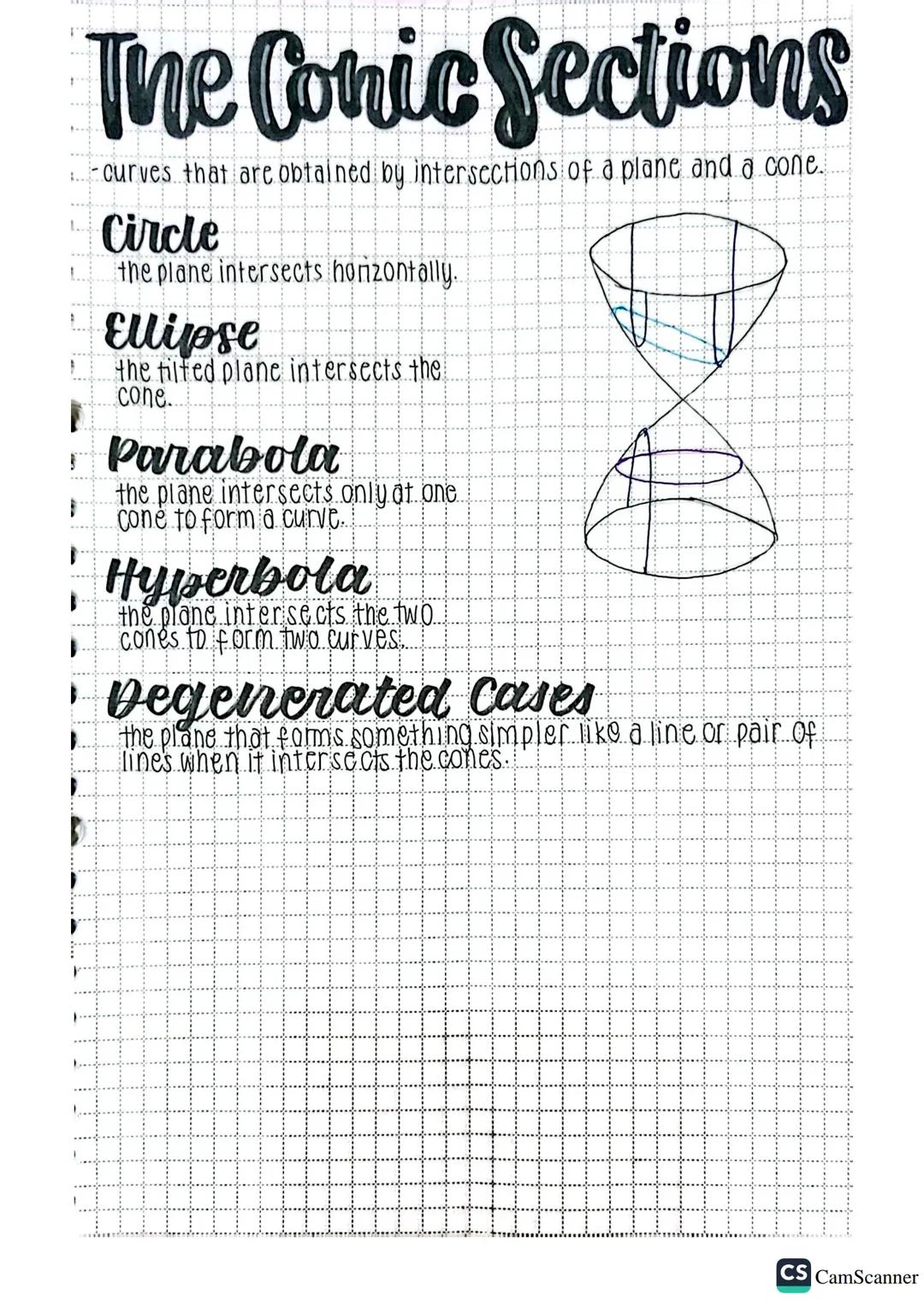
When a plane slices through a cone, it creates different curves depending on how the intersection happens. These resulting curves are called conic sections and they're crucial in both mathematics and real-world applications.
A circle forms when the plane cuts horizontally across the cone, creating a perfectly round shape. When the plane tilts slightly, it creates an ellipse - a stretched circle that describes planetary orbits and architectural arches.
A parabola occurs when the plane intersects only one cone, creating a U-shaped curve that explains the path of thrown objects or the shape of satellite dishes. When the plane intersects both parts of a double cone, it forms a hyperbola - two open curves that appear in navigation systems and cooling tower designs.
Quick Insight: Ever wonder why a flashlight creates circular, oval, or parabolic light patterns on different surfaces? That's conic sections in action!
There are also degenerated cases where the intersection creates simpler shapes like a point, a line, or a pair of lines. These special cases help mathematicians understand the boundaries between different conic sections.