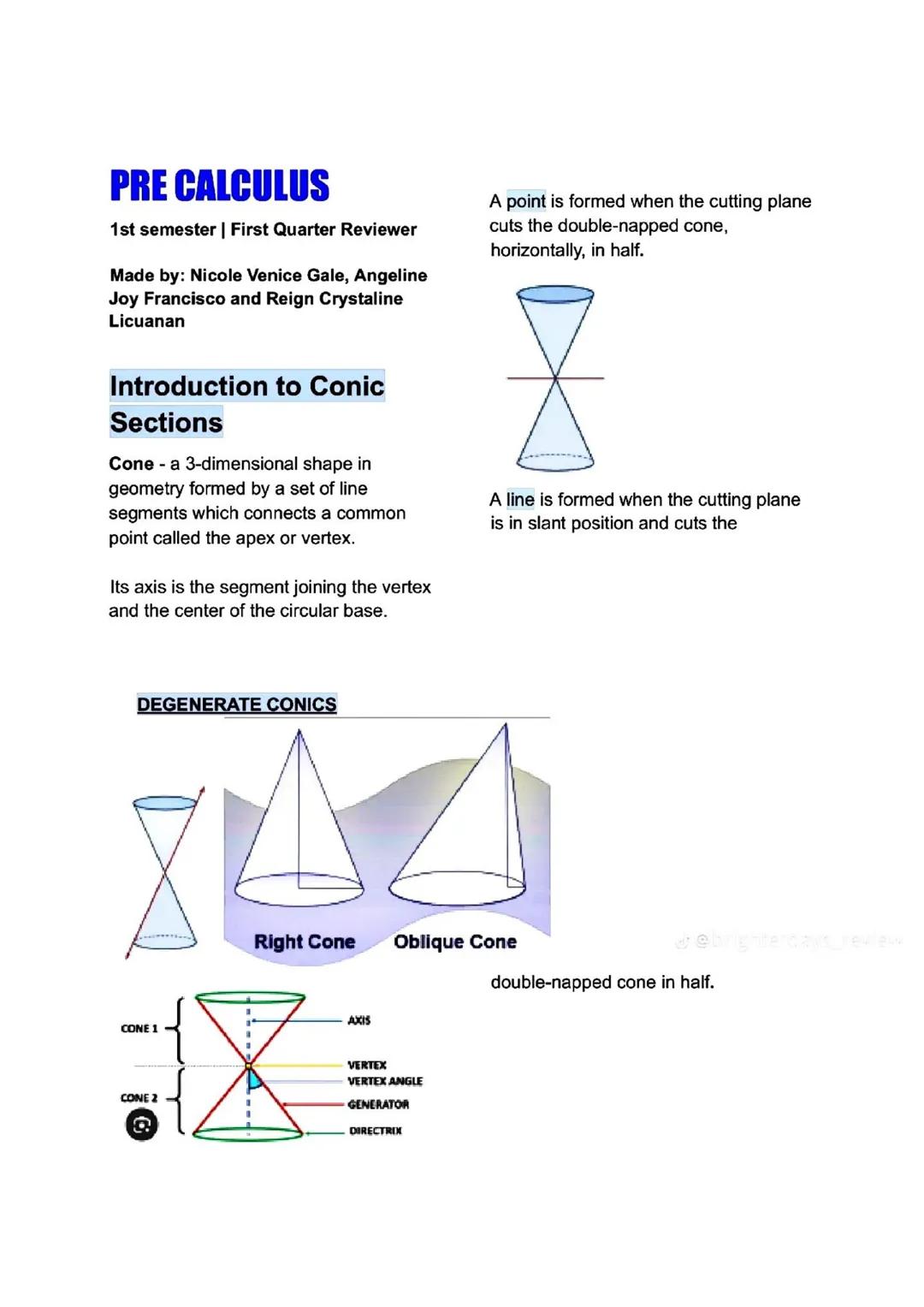
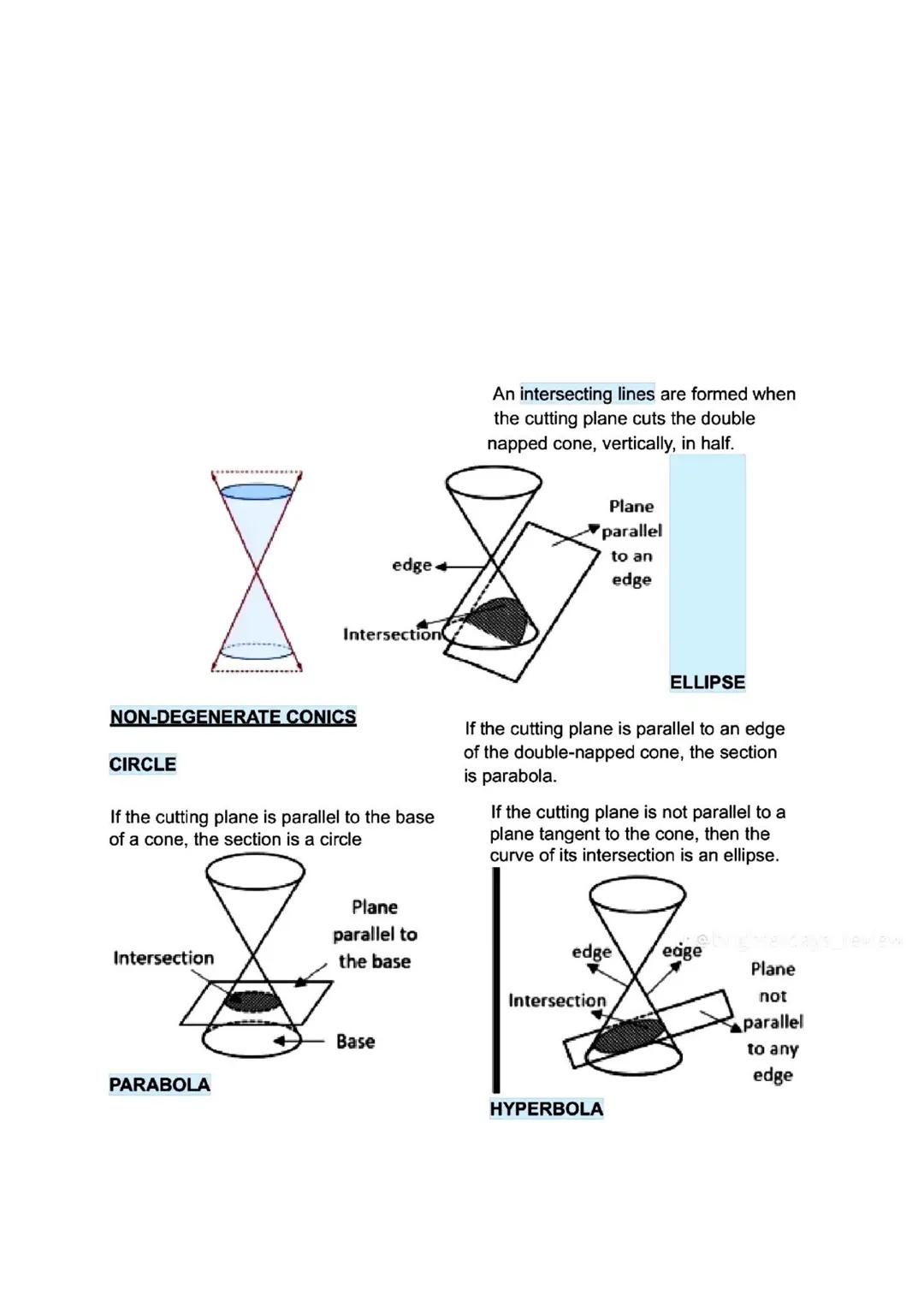
Parabolas and Ellipses - Getting Into the Details
Parabolas have some pretty specific rules. The standard forms depend on which direction they open: y² = 4ax opens right, y² = -4ax opens left, x² = 4ay opens up, and x² = -4ay opens down. The value 'a' tells you how far the focus is from the vertex.
When the vertex isn't at the origin, you use forms like y−k² = 4ax−h. The latus rectum is a special chord that passes through the focus and helps you graph the parabola accurately.
Ellipses are like squished circles with two special points called foci inside them. The amazing property? The sum of distances from any point on the ellipse to both foci is always constant! The major axis is the longer diameter, while the minor axis is the shorter one.
For ellipses, remember that a > b always, and if a = b, you actually have a circle. The relationship c² = a² - b² connects the center-to-focus distance (c) with the semi-major (a) and semi-minor (b) axes.
Study tip: For ellipses, whichever variable has the larger denominator determines whether it's horizontal or vertical!