What Are Conic Sections and Circles?

Think of conic sections as the shapes you'd see if you sliced through an ice cream cone with a knife at different angles. Conic sections include circles, parabolas, ellipses, and hyperbolas - each created by changing how the cutting plane intersects the cone.

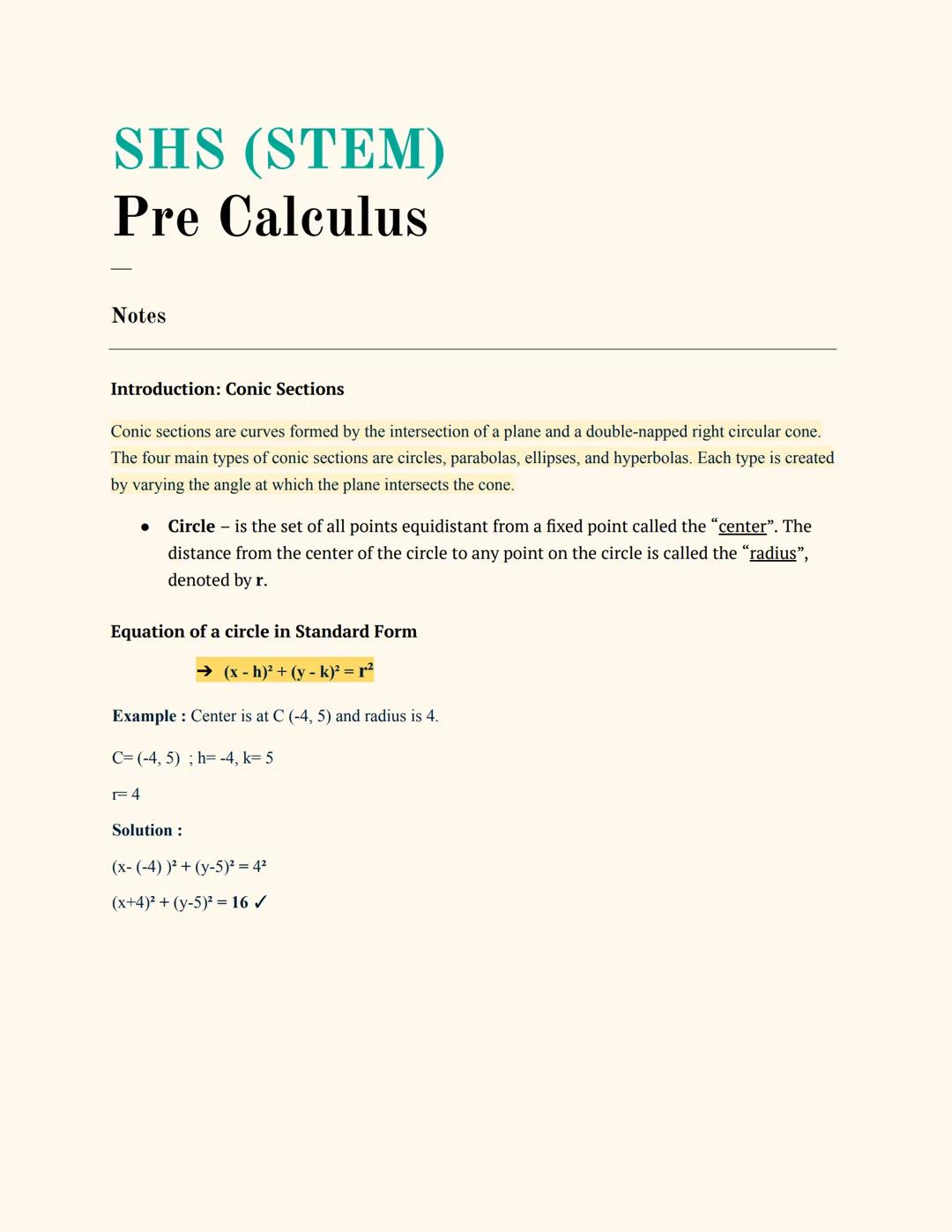
A circle is simply all the points that are exactly the same distance from a center point. That fixed distance is called the radius $r$, and it's the key to writing circle equations.

The standard form of a circle equation is $x-h$² + $y-k$² = r², where (h,k) is the center and r is the radius. For example, if your center is at $-4, 5$ with radius 4, you get: $x+4$² + $y-5$² = 16.

Pro Tip: Notice how $x-(-4)$ becomes $x+4$ - the signs can be tricky, so double-check your work!

Converting to General Form

Sometimes you need your circle equation in general form: x² + y² + Ax + By + C = 0. Converting from standard form is straightforward once you master the FOIL method.

Let's convert $x+4$² + $y-5$² = 16 to general form. First, expand each squared term using FOIL: $x+4$² = x² + 8x + 16, and $y-5$² = y² - 10y + 25.

Then substitute back into your equation: x² + 8x + 16 + y² - 10y + 25 = 16. Rearrange to get everything on one side: x² + y² + 8x - 10y + 25 = 0.

Quick Check: Your general form should always have x², y², and possibly x, y, and constant terms - but never any other powers!

Practice Problem Walkthrough

Let's work through finding both forms when given center $3, -5$ and radius 6. This builds your confidence for test problems!

For standard form: $x-3$² + $y+5$² = 36. Remember that subtracting a negative gives you addition, so $y-(-5)$ becomes $y+5$.

For general form, expand using FOIL: $x-3$² = x² - 6x + 9 and $y+5$² = y² + 10y + 25. Substituting gives us x² - 6x + 9 + y² + 10y + 25 = 36.

Simplify by combining like terms and moving everything to one side: x² + y² - 6x + 10y - 2 = 0.

Success Strategy: Always double-check your FOIL expansions - they're where most mistakes happen!

Mastering Larger Numbers

Working with bigger numbers like center $-9, 9$ and radius 10 follows the exact same process - just be extra careful with your arithmetic!

Standard form: $x+9$² + $y-9$² = 100. The larger radius means r² = 100, which keeps the math clean.

For general form, expand carefully: $x+9$² = x² + 18x + 81 and $y-9$² = y² - 18y + 81. Your equation becomes x² + 18x + 81 + y² - 18y + 81 = 100.

Combining and rearranging: x² + y² + 18x - 18y + 62 = 0. Notice how the constant term (62) comes from adding 81 + 81 - 100.

Final Tip: Larger numbers mean more chances for arithmetic errors - work slowly and check each step!