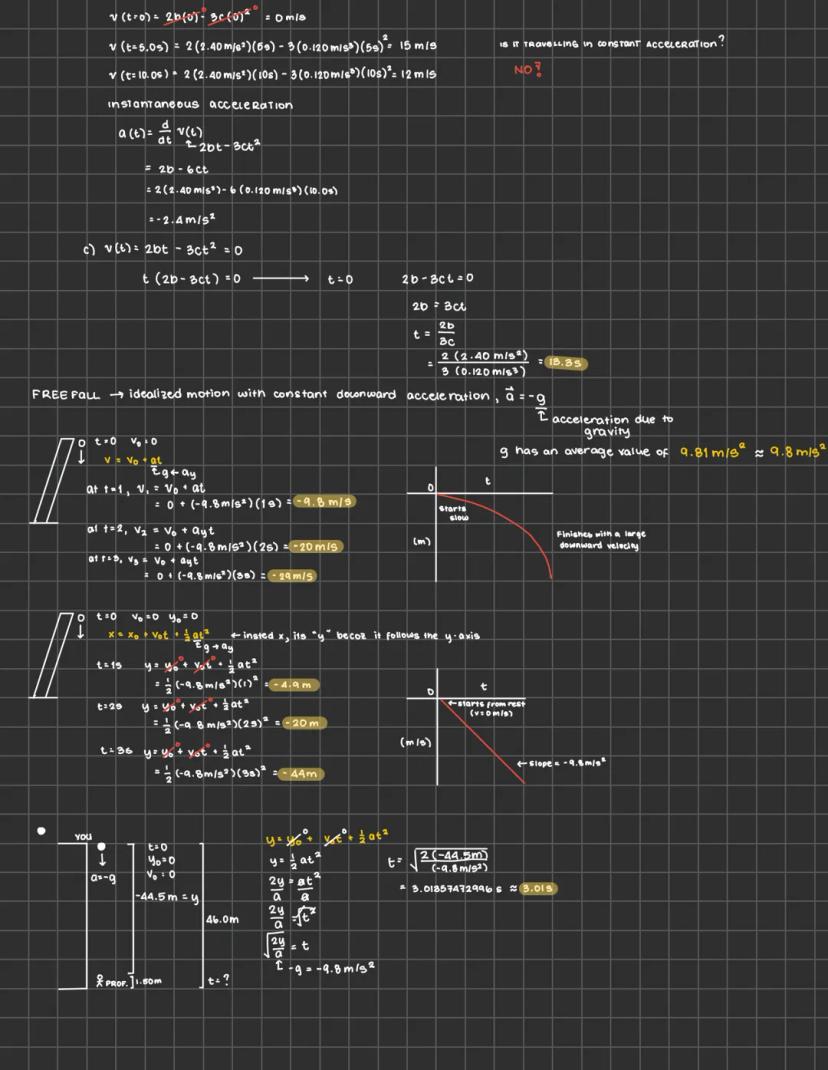
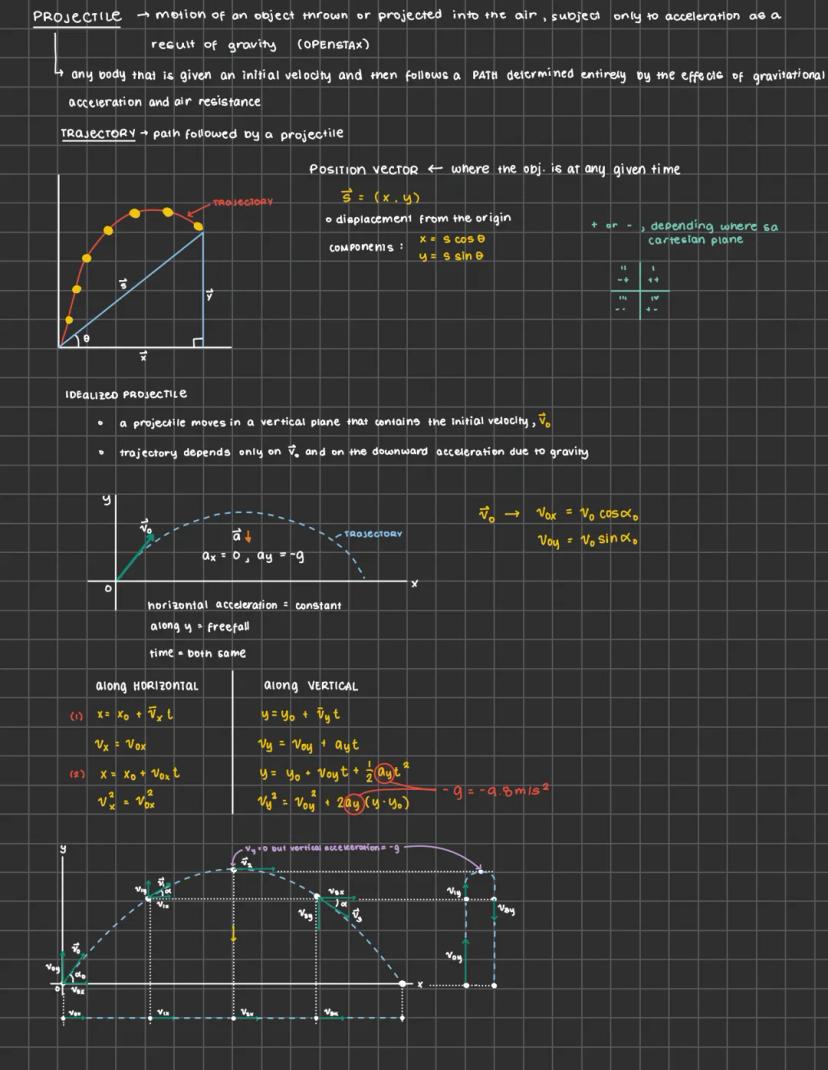
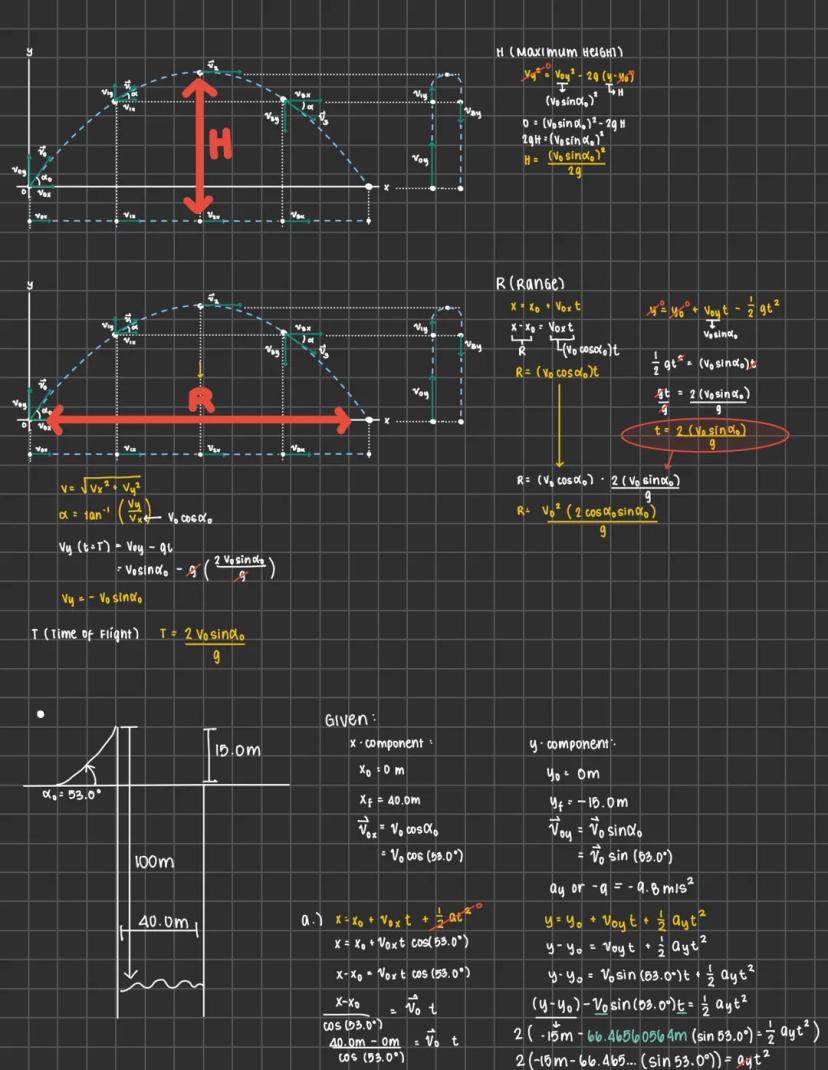
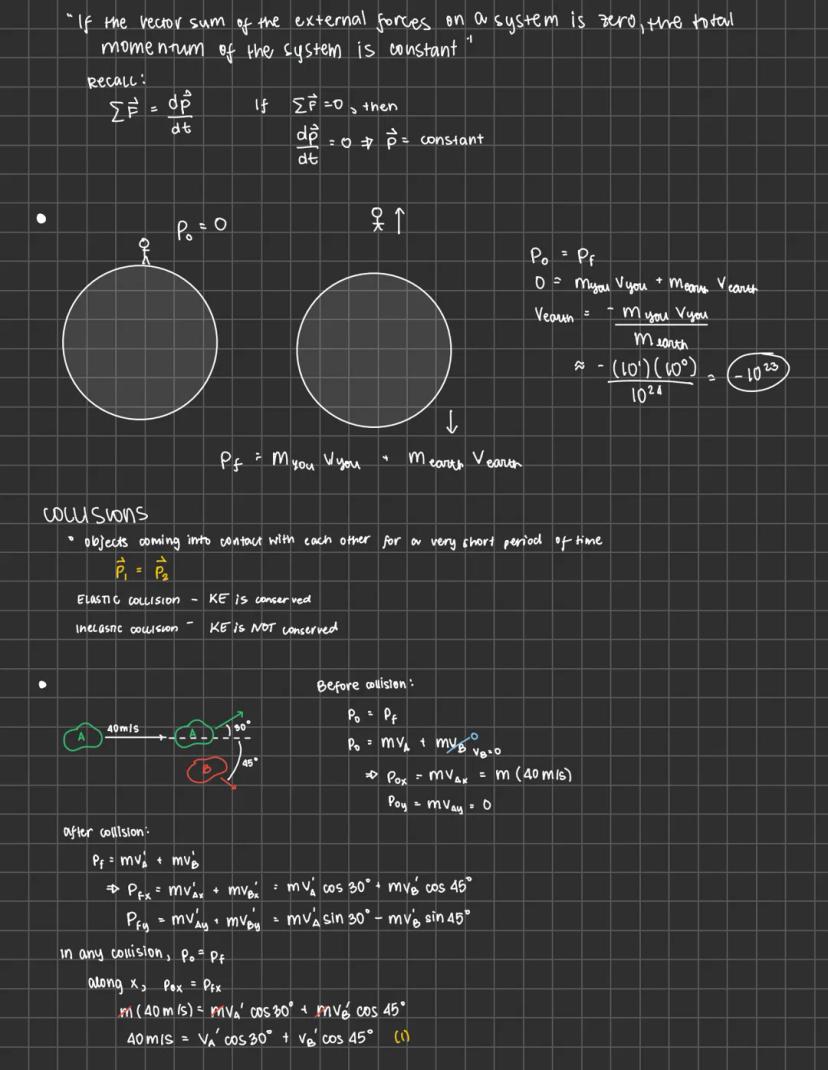
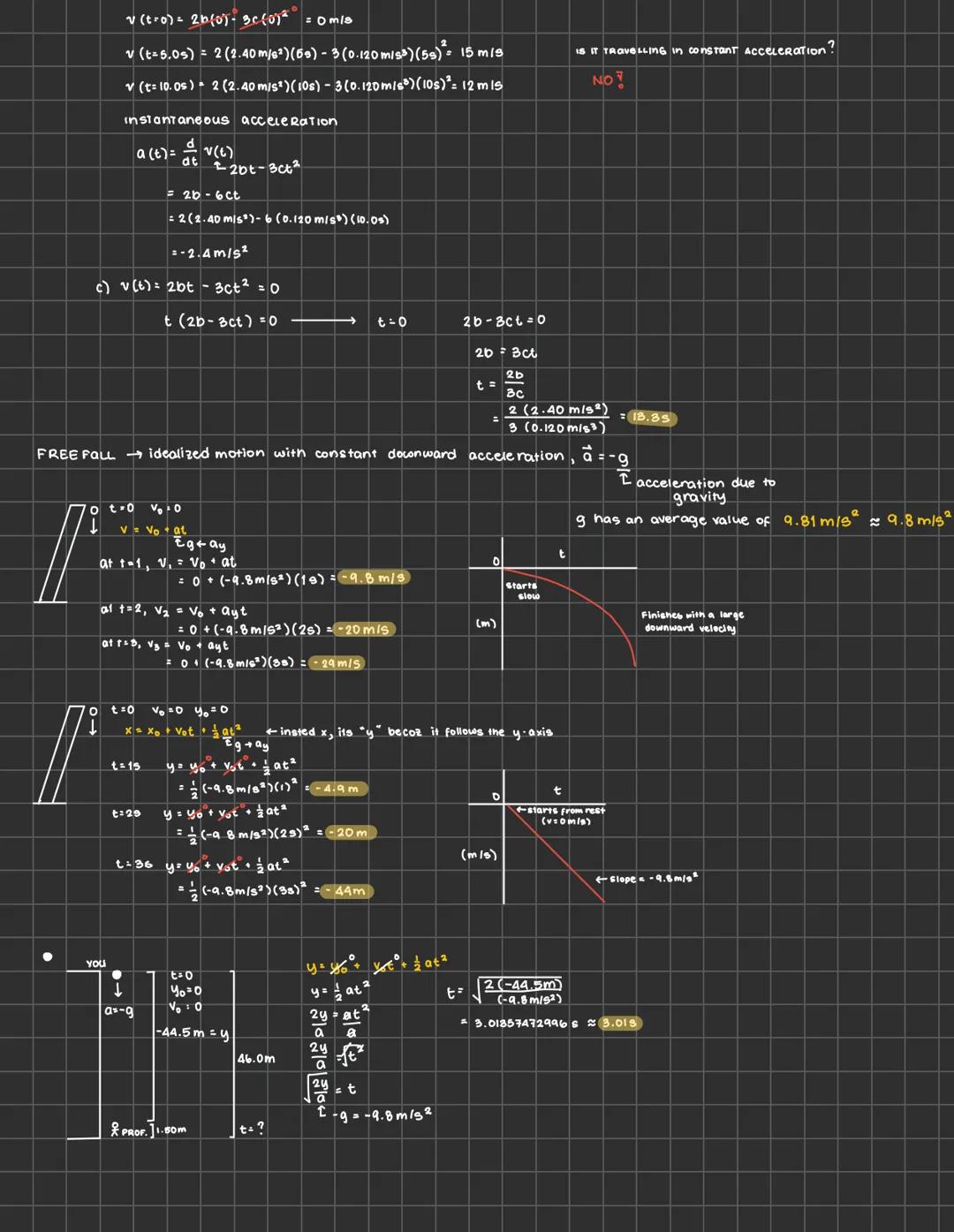
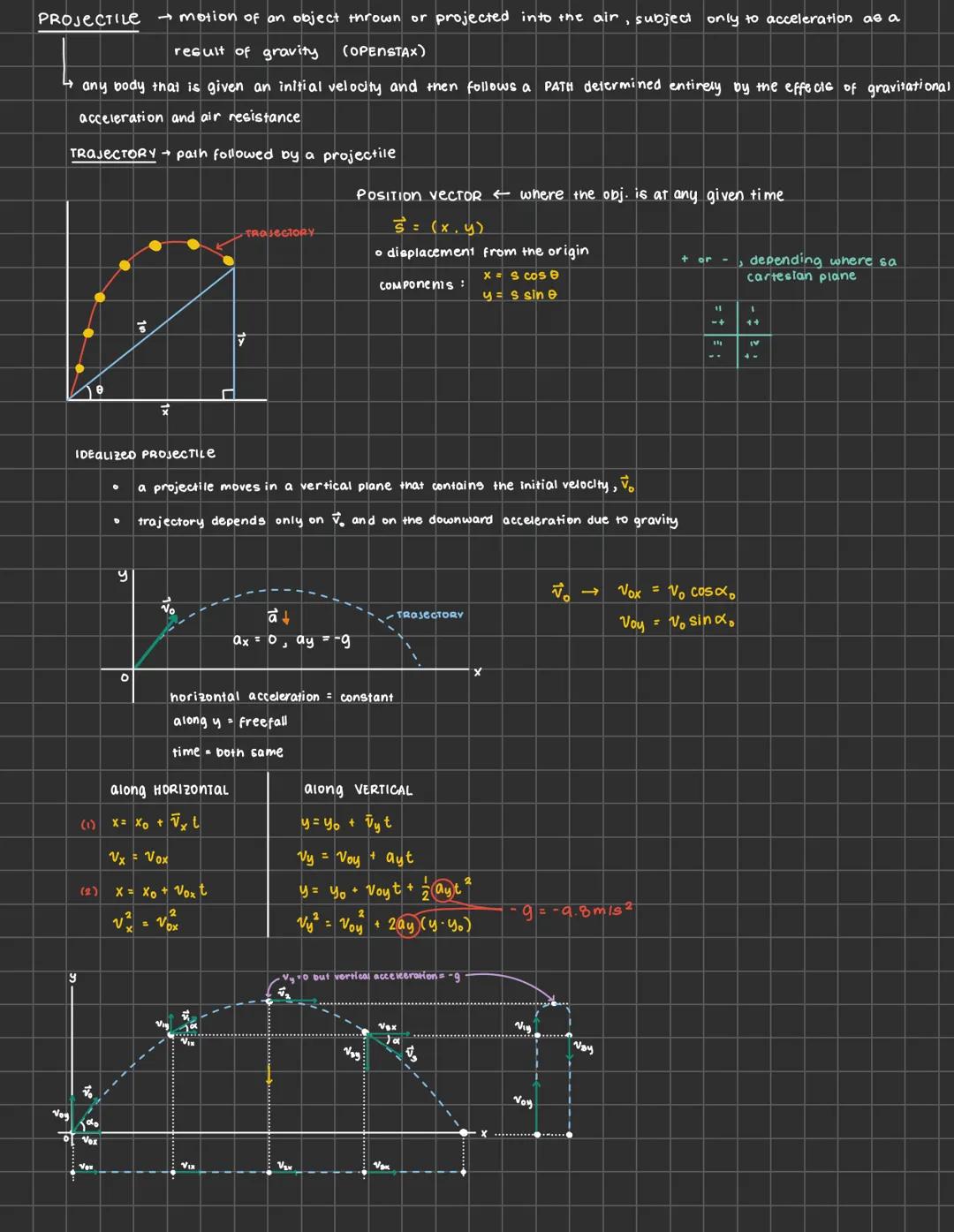
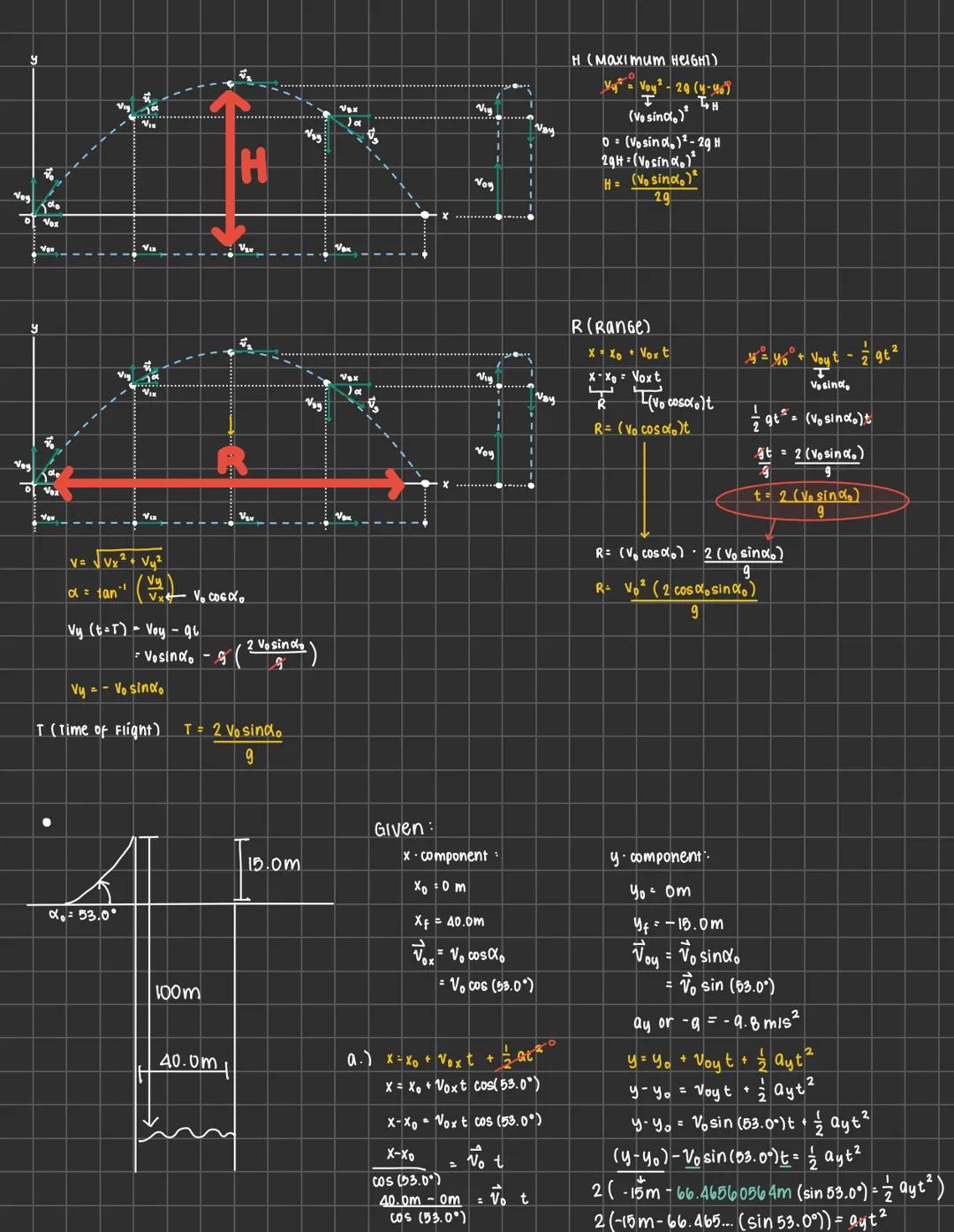
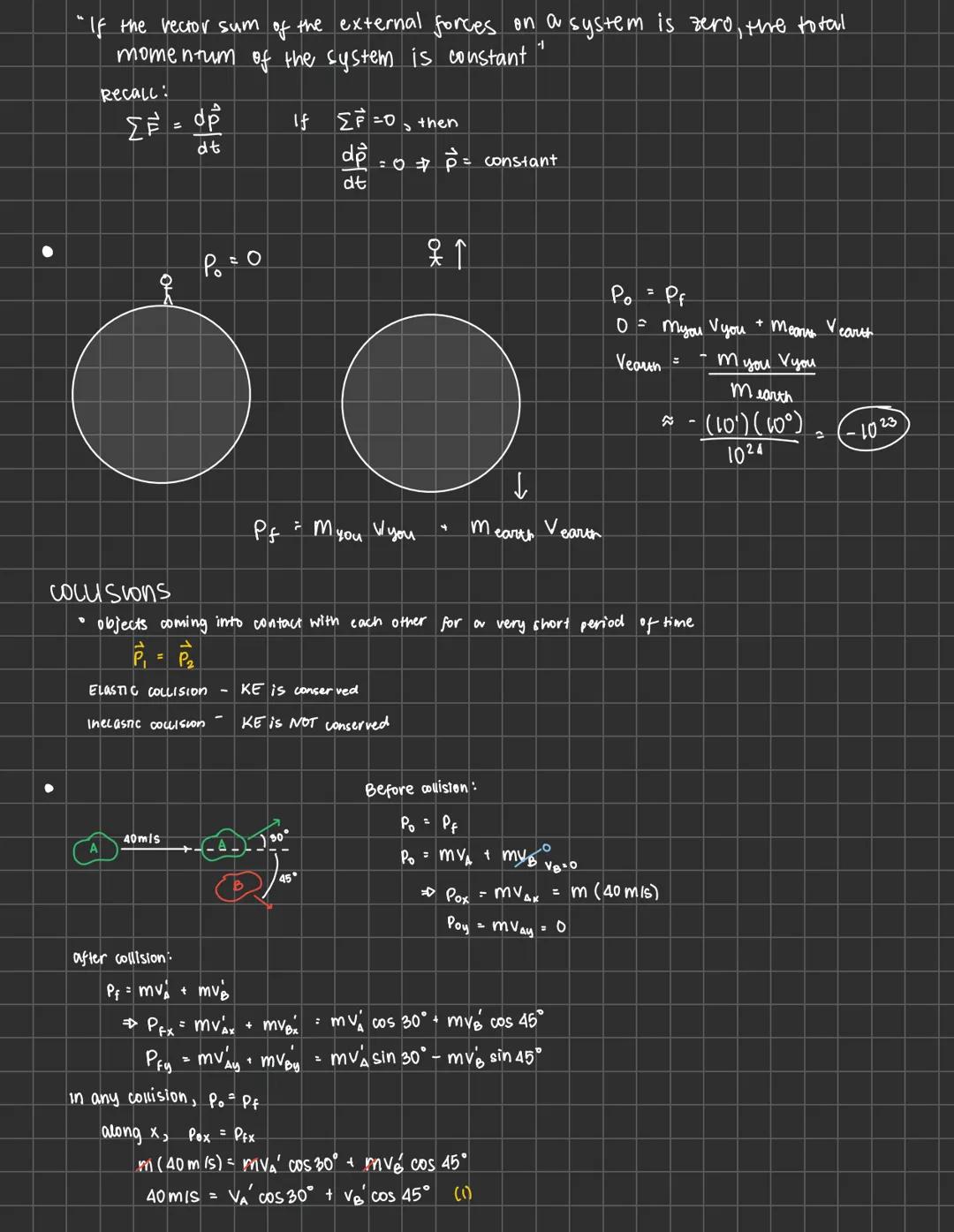
Physics can feel overwhelming, but mastering motion, forces, and energy... Ipakita pa
Mag-sign up para makita ang contentLibre ito!
Access sa lahat ng dokumento
Pagbutihin ang iyong mga grado
Sumali sa milyong mga estudyante
Sa pag-sign up, tinatanggap mo ang Terms of Service at Privacy Policy